航线的自动设计是电子海图应用的重要内容。近年来,如何设计安全、经济的航线成为众多学者关注的问题。最优航线就是在保证舰船航行安全的前提条件下,使航线达到某种指标上的最佳。如果仅从航行距离最短来考虑,最优航线是指求解一条安全的最短距离航线。已有的最短距离航线构建方法中,基于航路二叉树的最短距离航线自动生成方法应用较多,但也有其不足。针对航路二叉树方法存在的不足,本文改进了最短距离航线自动生成方法。
1航线自动生成方法的改进
1.1复杂碍航区的递归搜索
定义1测试点的最近相交碍航区:建立当前测试点到目的点之间的测试线,与测试线相交且距离当前测试点最近的碍航区(如图1,当前测试点S的最近相交碍航区为O1)。
定义2碍航区的左右路径点:对当前测试点建立测试线,作当前测试点的最近相交碍航区上各边界点与当前测试点之间的连线,根据绕行碍航区二分性特点,得到左右两条与测试线夹角最大的连线。左右两条连线与碍航区的切点称为碍航区的左右路径点(如图1,碍航区O1的左右路径点为A、B)。
复杂碍航区的递归搜索思想为:当前测试点构建的左(右)路径穿越碍航区(如O3)时,虚拟一个结点(虚拟结点与当前测试点具有相同的坐标信息)作为当前测试点的左(右)子结点,并将左(右)子结点作为新的当前测试点,新的当前测试点的最近相交碍航区为上述路径穿越的碍航区(如O3)。重复航路二叉树构建的过程,直到当前测试点的左(右)路径不再与任何碍航区相交。
在某些情况下,当前测试点与其最近相交碍航区的左右路径点的连线还可能与碍航区相交更复杂的情况,比如当前测试点S与碍航区O3的左右路径点(E、F)之间还可能与碍航区相交等,这种情形可能还会循环发生。不考虑当前结点选取对后续结点影响的处理方法,有可能造成最后所得的最短距离航线并非实际的最短距离航线。本文采用递归搜索法对这种复杂航路二叉树的情形进行了处理。以图1为例,具体步骤为:①如果当前测试点(如S)与目的点(如M)之间可直线航行,则结束循环;否则,找到当前测试点的最近相交碍航区(如O1)。②从当前测试点构建左(右)路径,如果准备构建的左(右)路径还与另外的碍航区相交(如当前测试点S的左路径SA与碍航区O3相交),则转③,否则(如当前测试点S的右路径SB不与碍航区相交)转④。③虚拟一个结点(如结点S′)作为当前测试点的左(右)子结点(S′与S具有相同的坐标信息)。虚拟结点对应的最近相交碍航区为与当前测试点左(右)路径相交的碍航区,以虚拟结点作为新的当前测试点。从当前测试点构建绕行其最近相交碍航区的左右两条路径,转②。④把当前测试点的最近相交碍航区的左(右)路径点(如碍航区O1的右路径点B)作为当前测试点的左(右)子结点,并将此左(右)子结点再作为新的当前测试点,转①。
按照上面步骤构建复杂碍航区的航路二叉树时,存在一些冗余路径。本文采用方向一致性判断法来避免冗余路径。
定义3碍航区的路径点:碍航区的左右路径点中的任何一个点称为碍航区的路径点。
定义4方向一致性判断法:如果测试点1的左(右)路径与碍航区相交,那么以该相交碍航区的左(右)路径点为测试点2。如果测试点2的最近相交碍航区与测试点1对应的最近相交碍航区相同,则测试点2只与测试点1的最近相交碍航区的左(右)路径点相连,右(左)路径点忽略。即同路径相连,异路径不相连。
1.2路径绕行碍航区的优化
针对绕行不规则碍航区存在路径穿越自身碍航区的情形,本文采用路径绕行碍航区的优化法解决这个问题。路径绕行碍航区的优化思想为:构建当前测试点的左(右)路径时,检测构建的左(右)路径是否与当前测试点所在的碍航区或者当前测试点的最近相交碍航区相交。如果相交,则把交点作为左(右)路径的中间航路点,修改左(右)路径。重复上述检测过程,直到左(右)路径不再与上述任一碍航区相交。
1.3特殊边界点的处理
特殊边界点的处理思想为:在航路二叉树的构建过程中,对一些不可能的特殊边界点进行动态检测,并提前结束存在特殊边界点的航路子二叉树的构建。由于研究区域的限制,可能造成当前海图只显示了碍航区的部分区域。如图2所示,碍航区的边P1P2为图廓的边界线,由于图幅划分或显示限制的原因,碍航区O1只显示了当前海图中的部分。航路二叉树构建过程中,如果不对这些特殊边界点(如图2中的P1、P2)进行处理,则可能使搜索的最短距离航线中包括这些特殊的边界点,从而出现不正确的结果。为了克服这个问题,采用边界检测法处理这些特殊边界点。在绕行碍航区的过程中,对当前测试点的左(右)路径进行判断,如果其中包含特殊边界点,则在左(右)路径中增加一个坐标最大值的中间航路点,然后结束左(右)路径航路子二叉树的构建。
1.4动态包络矩形分析
如果每次测试都对区域中的所有碍航区进行判断,则需要花费相对较长的时间。为了提高效率,采用动态包络矩形动态选取相关碍航区集,在每次测试中只需对相关碍航区集进行判断。获得动态包络矩形相关碍航区集的方法为:检测研究区域中的所有碍航区,如果存在碍航区与动态包络矩形相交或者包含时,则将该碍航区记录于动态包络矩形的相关碍航区集中。
1.5最短距离航线的提取
首先,采用递归法计算航路二叉树中每个结点到目的点的最短距离;其次,利用动态判断法求解最短距离航线;最后,优化最短距离航线。其中,在第一步中采用递归法获得最短距离时,隐含有对航路二叉树所有结点遍历的情形。
定义5结点的路径点集:结点与其对应碍航区的路径点之间的中间航路点集和结点的并集称为该结点的路径点集。
为了进行最短距离航线搜索,令d(X,Y)表示从结点X到结点Y之间的距离,D(X)表示从结点X到目的点M的最短距离。
1.5.1结点最短距离的求解
当前结点S的左右子结点都不为空时,则最短距离D(S)满足式(1):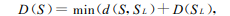
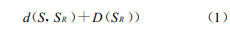
其中,S为当前结点;SL为当前结点的左子结点;SR为当前结点的右子结点。
当前结点S的左子结点为空,但右子结点不为空时,则D(S)满足式(2);当前结点S的右子结点为空,但左子结点不为空时,则D(S)满足式(3);当前结点S的左右子结点同时为空时,则D(S)满足式(4)。其中,M为目的点。
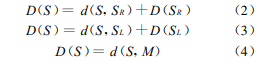
采用递归法求解任意结点到目的点的最短距离,具体步骤为:①如果结点(如S)的左右子结点都为空,则D(S)为d(S,M),结束。②如果结点(如S)的左子结点(如SL)为空,则D(S)等于d(S,SR)+D(SR);如果右子结点SR为空,则D(S)等于d(S,SL)+D(SL)。其中,D(SR)、D(SL)的求解转①。③如果结点(如S)的左右子结点都不为空,则D(S)等于min(d(S,SL)+D(SL),d(S,SR)+D(SR)),其中,D(SL)、D(SR)的求解转①。
1.5.2最短距离航线的动态判断法求解
如果当前结点到其左子结点的距离和左子结点到目的点之间的最短距离之和小于当前结点到其右子结点的距离和右子结点到目的点之间的最短距离之和,则取左子结点的路径点集作为最短距离路径,否则,取右子结点的路径点集作为最短距离路径
当前结点S的左右子结点都不为空时,若满足式(5),则记录当前结点S的路径点集于最短距离路径数组中,并将SL作为新的当前结点;若满足式(6),则记录当前结点S的路径点集于最短距离路径数组中,并将SR作为新的当前结点;
(d(S,SL)+D(SL))<(d(S,SR)+D(SR))(5)
(d(S,SL)+D(SL))≥(d(S,SR)+D(SR))(6)
当前结点S的左子结点为空,但右子结点不为空时,则记录当前结点S的路径点集于最短距离路径数组中,并将SR作为新的当前结点。
当前结点S的右子结点为空,当左子结点不为空时,则记录当前结点S的路径点集于最短距离路径数组中,并将SL作为新的当前结点。当前结点S的左右子结点同时为空时,则记录当前结点S的路径点集和目的点于最短距离路径数组中。
最短距离航线的航路点集记录于mNavLNode数组中。以起始点S为当前结点,根据动态判断法搜索最短距离航线路径的具体步骤为:①如果当前结点(如S)的左右子结点都为空,则将当前结点的路径点集和目的点记录于mNavLineNode,结束。②如果当前结点(如S)的左子结点SL(右子结点SR)为空,则将当前结点的路径点集记录于mNavLineNode,并将SR(SL)作为新的当前结点,转①。③如果当前结点(如S)的左右子结点都不为空,则将当前结点的路径点集记录于mNavLineNode。如果d(S,SL)+D(SL)小于d(S,SR)+D(SR),则将SL作为新的当前结点,转(1);否则,将SR作为新的当前结点,转①。
至此,mNavLineNode中记录了最短距离航线路径点集。
1.5.3最短距离航线的优化
mNavLineNode数组中存储最短距离航线的航路点集,由于对复杂碍航区进行递归搜索,mNavLineNode中可能存在坐标相同的点,因此,必须删除坐标相同的点。如果所得最短距离航线中的某两个航路点之间还可以直线航行,还必须删除中间的冗余航路点。
2实验与分析
本文针对复杂碍航区的情形,分别应用航路二叉树方法和本文方法在CPU主频为2.66GHz、内存为2G的计算机上进行比对实验,实验结果如图3和表1所示。

图3中显示的折线分别为采用不同方法获得的最短距离航线。如图3所示,基于航路二叉树方法所得的最短距离航线里程为162.55km,转向点数为5,而使用本文方法所得的最短距离航线里程为144.23km,转向点数为3。
由实验可知,本文方法克服了航路二叉树方法对复杂碍航区处理不完备的问题,进一步优化了航线绕行碍航区的策略。
同时,从表1中也可以看出,本文方法相对已有的航路二叉树方法,在效率上也有明显提高。
3结语
本文通过复杂碍航区路径的递归搜索和碍航区的绕行优化,实现了复杂碍航区的航线自动生成,利用方向一致性判断、边界检测和动态包络矩形排斥等策略优化航线生成,利用递归和动态判断法求解最短距离航线。实验结果证明,此方法合理可行,能够从复杂碍航区自动选取一条最短距离航线,在自动生成航线的质量和效率上都有明显提高。当然,对于航线设计,还应考虑水文气象等动态因素的影响,这有待于以后的进一步研究。

